有限要素法の基本的
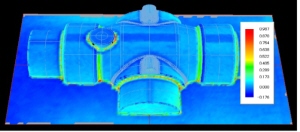
有限要素法(Finite Element Method、FEM)は、連続体の物理的・数学的な問題を近似的に解くための数値解析手法の一つです。この手法は、構造解析、熱伝導、流体力学、電磁気学などの多くの工学分野で使用されています。
有限要素に従って基本的な考え方は、連続体を小さな要素(有限要素)に分割(離散化)し、それぞれの要素の振る舞いを近似的に計算して全体の振る舞いを推定することです。
以下は、有限要素法の基本的な手順です:
- 離散化:解きたい領域を小さな要素に分割します。一般的には、領域は三角形や四辺形、四面体、六面体などの形状の要素に分割されます。
- 要素方程式の導出:各要素の振る舞いを近似的に表現するための方程式を導出します。
- 組み立て:各要素の方程式を一つの大きなシステム方程式に組み立てます。
- 境界条件の適用: 問題に与えられた境界条件や初期条件をシステム方程式に適用します。
- 方程式の解: 得られた方程式システムを数値的に解きます。このステップで、未知の変数の近似的な値が得られます。
- 結果の解釈: 得られた数値解を用いて、物理的または構造的な振る舞いを解釈または中断します。
有限要素法適用は、非常に複雑な形状や境界条件を持つ実際の問題に適用可能なことである。 ただし、正確な解を得るためには、適切な要素の選択、離散化の精度、境界条件の設定など、多くの配慮を考慮する必要があります。
| <3Dスキャンに戻る> |
